Process control Ziegler-Nichols PID Tuning Method
A control system with a Ziegler-Nichols PID controller is represented as shown below.
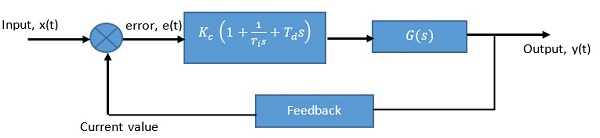
The Ziegler-Nichols rule for PID loop tuning is used to obtain approximate values for three gain parameters of the PID controller: the controller’s path gain, Kp, the derivative time constant, Td and integrator time constant, Ti. From the feedback transfer function of the system, the gain margin, Ku and the period of oscillation, Tu at the system stability limits are measured and used for tuning the PID parameters. The goal of Ziegler-Nichols PID tuning is to achieve good disturbance rejection.
In the MATLAB Code attached, the plant transfer function, G(s) is first generated from the inputs entered by the user (numerator and denominator of the transfer function). The plant transfer function is used to obtain the closed loop margins (Ku and Tu). The margins are used to calculate the critical path gain (Kc), integrator time (Ti) and the derivative time (Td) to be used for the Ziegler-Nichols PID tuning. For a classical Ziegler-Nichols controller, the values are calculated as: Kc=0.6 ×Ku,; Ti=0.5 × Tu; Td=0.125 ×Tu
The Ziegler-Nichols PID controller is then obtained as: Wc=Kc (1+1/(Ti s)+Td s). The compensated closed loop response is obtained by combining the Ziegler-Nichols controller in series with the plant in a unity feedback system as CLTF=feedback(series(G,Wc ),1)
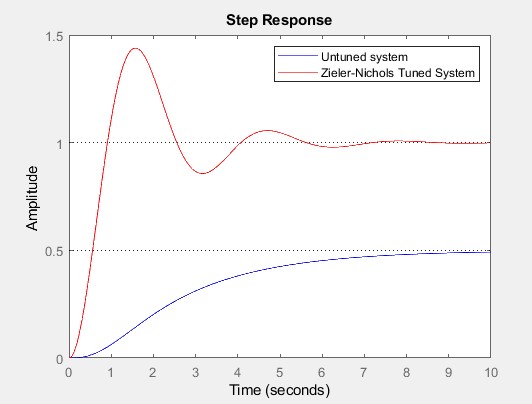
As an example, the step response of the uncompensated and compensated (controlled) systems for a third-order system transfer function, G=1/(s3+4s2+6s+1) is shown in the figure below:
%% To run the code, write the function name into the command window
% For Example:
%.........Ziegler_NicholsPID
%............and press enter
%% Inputs to the Ziegler Nichols PID Tuner
% num : Numerator(starting from highest order of coefficients)in
% form of []
% den : Denomerator(starting from highest order of coefficients)in
% form of []
function ZN =Ziegler_NicholsPID()
num=input("Enter the numerator of the open-loop system transfer function, num : ");
den=input("Enter the denominator of the open-loop system transfer function, den : ");
G=CreatePlant(num,den) %Plant transfer function
G1=feedback(G,1);
[Kcr,Pm,Wcg,Wcm]=margin(G1); %Finding margins of the uncompensated system
Tcr=2*pi/Wcg; %Finding the time from the gain margin frequency.
Kc=0.6*Kcr; %Critical gain
Ti=0.5*Tcr; %Reset time (minutes)
Td=0.125*Tcr; %Derivative time (minutes)
%Creating Ziegler-Nichols PIDController transfer function
Wc=ZieglerNicholsPIDController( Kc,Ti,Td )
%Closed loop system function with Z-N controller in series with the
%plant
CLTF=feedback(series(G1,Wc),1)
% Wp : Plant transfer function
% Wc : Ziegler-Nichols PIDController transfer function
% CLTF : Closed Loop transfer function (H=1, Unity feedback).
t=0:0.01:10;
figure (1)
step(G1,t, 'b')
hold on
step(CLTF,t, 'r')
hold off
legend ("Untuned system","Zieler-Nichols Tuned System")
end
%% Creating the plant to control
%CreatePlant will create the open loop plant's transfer function with the
%num and denomitor values entered
function [ Plant ] = CreatePlant( num,den )
syms s;
Plant=tf(num,den);
end
%% ZieglerNicholasPIDController function to generate the PID controller transfer function
function Wc = ZieglerNicholsPIDController( Kc,Ti,Td )
%Parameters
% Kc : Critical gain
% Ti : Reset time (minutes)
% Td : Derivative time (minutes)
% Wc : Ziegler-Nichols PID controller in Laplace
s=tf('s');
Wc=Kc*(1+(1/(Ti*s))+Td*s);
end
Buy Process control Ziegler-Nichols PID Tuning Method Assignment Answers Online
Talk to our expert to get the help with Process control Ziegler-Nichols PID Tuning Method Assignment to complete your assessment on time and boost your grades now
The main aim/motive of the management assignment help services is to get connect with a greater number of students, and effectively help, and support them in getting completing their assignments the students also get find this a wonderful opportunity where they could effectively learn more about their topics, as the experts also have the best team members with them in which all the members effectively support each other to get complete their diploma assignments. They complete the assessments of the students in an appropriate manner and deliver them back to the students before the due date of the assignment so that the students could timely submit this, and can score higher marks. The experts of the assignment help services at urgenthomework.com are so much skilled, capable, talented, and experienced in their field of programming homework help writing assignments, so, for this, they can effectively write the best economics assignment help services.

