Solving Equations Homework Help
Previous
Next
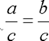
, where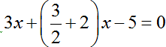
Steps to solve one variable linear equation:
Step 1:
The parentheses involved in the equations are removed by applying the distributive property and the fractions are eliminated by multiplying each side by LCD of that fractions.
Step 2:
Use the properties and retain the unknown variable on one side and shift the remaining terms on the other side.
Step 3:
Perform the elementary calculations to obtain the solution.
Example 1:
Consider the equation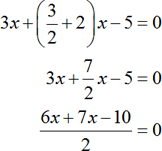
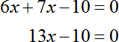
Multiply both sides by 2.
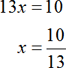
Isolate x variable.
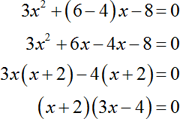
Solving one variable quadratic equations:
A quadratic equation is a single variable polynomial equation of order 2 in the form ax2+bx+c=0 with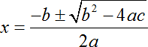
where a,b,c are constants and x is unknown variable.
Using factor method or quadratic formula to solving this equation.
Factoring a quadratic equation:
Step 1: Consider the equation ax2+bx+ c=0
Step 2: Multiply the a term of the co-efficient of x2 with constant c term.
Step 3: Obtain two factors r and s, that multiplies together to get ac and add together to get b.
Step 4: Replace the middle term bx with the factors (r+ s)x.
Step 5: Solve by grouping. That is taking the equation in two groups. Obtain the GCF from each group. Take the similar groups and combine remaining terms.
Step 6: Equate zero to the factors gives the required two solutions (roots).
Example 2:
Consider the polynomial 3x2+2x–8=0.
The product of 3 and − 8; is −24. Thus, obtain factors such that their product is - 24 and the sum is 2. Therefore, the factors are 6 and−4.
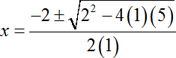
Equating the factors to zero.
(x+2)=0 or (3x−4)=0
Thus, the solutions are x=–2and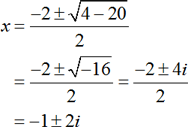
.
Solving quadratic equation by using formula:
The quadratic formula is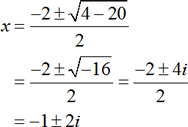
.
Example 3:
Consider a quadratic equation x2+2x+5=0 . Since the given quadratic equation cannot be factored easily, the required roots can be obtained by using quadratic formula method as follows:
Here a=1,b=2,and c=5.
Therefore,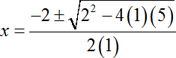
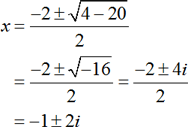
Here, the roots are complex. That is, x1=–1+2i and x2=–1–2i.
Solving one variable higher degree equation:
The equation with degree up to 5 can be solved by using the rational root theorem, which helps to obtain one factor and then the remaining expression can be reduced to lower degree equation by using synthetic division or long division method. Continue this process (or apply factor method) until all the roots are obtained.
Suppose the degree of the equation is higher (greater) than 5, then rational root theorem works can be applied only to solve few simple problems. Thus, in order to solve the complex problems, various methods or techniques can be applied say, numerical methods like Newton-Raphson method or Root-finding algorithms can be used to obtain the roots.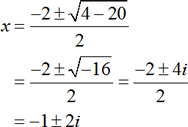
Solving Equations
The linear one variable equation is of the form, ax+b=c where a,b and c are constants. The solution of the equation is satisfied that equation. The linear equations can be simplified by using the below properties:
1. If a=b, then a+c=b+ c.
2. If a=b, then a−c=b− c.
3. If a=b, then ac=bc.
4. If a=b, then
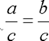
, where
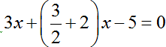
Steps to solve one variable linear equation:
Step 1:
The parentheses involved in the equations are removed by applying the distributive property and the fractions are eliminated by multiplying each side by LCD of that fractions.
Step 2:
Use the properties and retain the unknown variable on one side and shift the remaining terms on the other side.
Step 3:
Perform the elementary calculations to obtain the solution.
Example 1:
Consider the equation
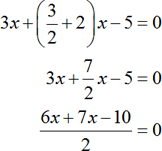
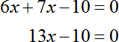
Multiply both sides by 2.
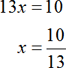
Isolate x variable.
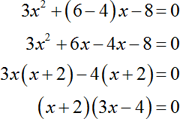
Solving one variable quadratic equations:
A quadratic equation is a single variable polynomial equation of order 2 in the form ax2+bx+c=0 with
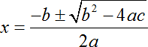
where a,b,c are constants and x is unknown variable.
Using factor method or quadratic formula to solving this equation.
Factoring a quadratic equation:
Step 1: Consider the equation ax2+bx+ c=0
Step 2: Multiply the a term of the co-efficient of x2 with constant c term.
Step 3: Obtain two factors r and s, that multiplies together to get ac and add together to get b.
Step 4: Replace the middle term bx with the factors (r+ s)x.
Step 5: Solve by grouping. That is taking the equation in two groups. Obtain the GCF from each group. Take the similar groups and combine remaining terms.
Step 6: Equate zero to the factors gives the required two solutions (roots).
Example 2:
Consider the polynomial 3x2+2x–8=0.
The product of 3 and − 8; is −24. Thus, obtain factors such that their product is - 24 and the sum is 2. Therefore, the factors are 6 and−4.
Equating the factors to zero.
(x+2)=0 or (3x−4)=0
Thus, the solutions are x=–2and
.
Solving quadratic equation by using formula:
The quadratic formula is
.
Example 3:
Consider a quadratic equation x2+2x+5=0 . Since the given quadratic equation cannot be factored easily, the required roots can be obtained by using quadratic formula method as follows:
Here a=1,b=2,and c=5.
Therefore,
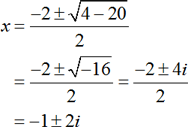
Here, the roots are complex. That is, x1=–1+2i and x2=–1–2i.
Solving one variable higher degree equation:
The equation with degree up to 5 can be solved by using the rational root theorem, which helps to obtain one factor and then the remaining expression can be reduced to lower degree equation by using synthetic division or long division method. Continue this process (or apply factor method) until all the roots are obtained.
Suppose the degree of the equation is higher (greater) than 5, then rational root theorem works can be applied only to solve few simple problems. Thus, in order to solve the complex problems, various methods or techniques can be applied say, numerical methods like Newton-Raphson method or Root-finding algorithms can be used to obtain the roots.
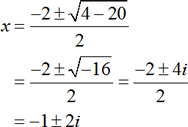
Solving Equations, math homework help, Math Assignment Help, Help For Math Homework, Mathematics Homework Help, Mathematics Assignment Help,online math homework help,math homework helper,help my math homework,help with math problems, Maths Tutorials
Math Tutorials
- Math - Polynomials
- Math - Series and Sequences
- Math - Dividing Polynomials
- Math - Factoring Polynomials
- Math - Solving Quadratics
- Math - Solving Inequalities
- Math - Solving Equations
- Math - Complex Numbers
- Math - Matrix
- Math - Inverse Functions
- Math - Graphing Quadratic Functions
- Math - Graphing Polynomial Functions
- Math - Functions
- Math - Exponentials and Logarithms
- Math - Cramer's Rule
- Math - Absolute Value & Inequalities

